
Logistic regression is an extremely robust and flexible method for dichotomous classification prediction that is, it is used to predict for a binary outcome or state, such as yes/ no, success/ failure, and will occur/ won’t occur. In a study on QSAR nanotoxicity of nanoparticles 35 in PaCa2 (pancreatic cancer cells), a consensus model consisting of logistic regression, Naïive Bayes, kNN, and SVM was developed with PADEL-Descriptor version 2.8 generated 1D and 2D chemical descriptors basing on SMILES, lipophilicity, and hydrogen bonding.Įric Benjamin Seufert, in Freemium Economics, 2014 Logistic regression
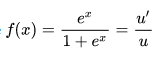
Logistic regression was also used in consensus models with other techniques to increase prediction capabilities. 34 Both models were validated internally and externally and LR has outperformed LDA for compounds that exhibit excess toxicity versus nonpolar narcotic compounds and for more reactive compounds versus less reactive compounds. They used experimental data and chemical structure-based descriptors calculated by the CODESSA and DRAGON software packages. have compared logistic regression with another interpretable model, linear discriminant analysis (LDA) model in aquatic toxicity prediction. This issue can be, however, solved by penalization of the weights or defining a prior probability distribution of weights.

In cases when a feature correctly separating two classes in the first iteration is found, data are not separated further. Logistic regression is also prone to restrictive expressiveness and complete separation. In this case, the approach with a smaller number of classes provided better accuracy. The paper has shown that test set accuracy can vary strongly depending on the initial classification of the training set (whether we have separate classes for different strengths of sensitization, or we have a binary “weak or nonweak” classification). 33 The training set consisted of 196 compounds, and the test set contained 22 compounds divided into four sensitizers classes: weak, moderate, strong, and extreme. applied logistic regression to predict skin sensitization with use of data from murine Local Lymph Node Assay studies and similarity 4D-fingerprint descriptors. In QSAR toxicity modeling, logistic regression has found multiple applications. The main obstacle is the multiplicative nature of the “odds.” One can say that the interpretability of logistic regression is not as easy as the interpretation of kNN or linear regression, but still much easier than more “black-box” models such as Neural Networks. In contrary to linear regression, the relationship between the weights and the output of the model (the “odds”) is exponential, not linear. Just as in linear regression, logistic regression has weights associated with dimensions of input data. The mathematics of logistic regression rely on the concept of the “odds” of the event, which is a probability of an event occurring divided by the probability of an event not occurring. The binary logistic model classifies specimen into two classes, whereas the multinomial logistic model extends this to an arbitrary number of classes without ordering them. In the basic version of logistic regression, the output variable is binary, however, it can be extended into multiple classes (then it is called multinomial logistic regression). It takes a linear combination of features and applies to them a nonlinear sigmoidal function. Its most significant advantage is that it can be used both for classification and class probability estimation, because it is tied with logistic data distribution.
Logistic regression is another fundamental method initially formulated by David Cox in 1958 32 that builds a logistic model (also known as the logit model). Aleksandra Bartosik, Hannes Whittingham, in The Era of Artificial Intelligence, Machine Learning, and Data Science in the Pharmaceutical Industry, 2021 Logistic regression


 0 kommentar(er)
0 kommentar(er)
